Analog Communication Con 2......

Mathematical Expressions

Following are the mathematical expressions for these waves.

Time-domain Representation of the Waves

Let the modulating signal be,

m(t)=Amcos(2πfmt)$$m\left(t\right)=A_m\cos \left(2\pi f_{m}t\right)$$

and the carrier signal be,

c(t)=Accos(2πfct)$$c\left(t\right)=A_c\cos \left(2\pi f_{c}t\right)$$

Where,

Am$A_m$ and Ac$A_c$ are the amplitude of the modulating signal and the carrier signal respectively.

fm$f_m$ and fc$f_c$ are the frequency of the modulating signal and the carrier signal respectively.

Then, the equation of Amplitude Modulated wave will be

s(t)=[Ac+Amcos(2πfmt)]cos(2πfct)$s(t)=\left[A_c+A_m\cos \left(2\pi f_{m}t\right)\right]\cos \left(2\pi f_{c}t\right)$ (Equation 1)

Modulation Index

A carrier wave, after being modulated, if the modulated level is calculated, then such an attempt is called as Modulation Index or Modulation Depth. It states the level of modulation that a carrier wave undergoes.

Rearrange the Equation 1 as below.

s(t)=Ac[1+(AmAc)cos(2πfmt)]cos(2πfct)$s(t)=A_c\left[1+\left(\frac{A_m}{A_c}\right)\cos \left(2\pi f_{m}t\right)\right]\cos \left(2\pi f_{c}t\right)$

⇒s(t)=Ac[1+μcos(2πfmt)]cos(2πfct)$\Rightarrow s\left(t\right)=A_c\left[1+\mu \cos \left(2\pi f_{m}t\right)\right]\cos \left(2\pi f_{c}t\right)$ (Equation 2)

Where, μ$\mu$ is Modulation index and it is equal to the ratio of Am$A_m$ and Ac$A_c$. Mathematically, we can write it as

μ=AmAc$\mu =\frac{A_m}{A_c}$ (Equation 3)

Hence, we can calculate the value of modulation index by using the above formula, when the amplitudes of the message and carrier signals are known.

Now, let us derive one more formula for Modulation index by considering Equation 1. We can use this formula for calculating modulation index value, when the maximum and minimum amplitudes of the modulated wave are known.

Let Amax$A_{max}$ and Amin$A_{min}$ be the maximum and minimum amplitudes of the modulated wave.

We will get the maximum amplitude of the modulated wave, when cos(2πfmt)$\cos \left(2\pi f_{m}t\right)$is 1.

⇒Amax=Ac+Am$\Rightarrow A_{max}=A_c+A_m$ (Equation 4)

We will get the minimum amplitude of the modulated wave, when cos(2πfmt)$\cos \left(2\pi f_{m}t\right)$is -1.

⇒Amin=Ac−Am$\Rightarrow A_{min}=A_c-A_m$ (Equation 5)

Add Equation 4 and Equation 5.

Amax+Amin=Ac+Am+Ac−Am=2Ac$$A_{max}+A_{min}=A_c+A_m+A_c-A_m=2A_c$$

⇒Ac=Amax+Amin2$\Rightarrow A_c=\frac{A_{max}+A_{min}}{2}$ (Equation 6)

Subtract Equation 5 from Equation 4.

Amax−Amin=Ac+Am−(Ac−Am)=2Am$$A_{max}-A_{min}=A_c+A_m-\left(A_c-A_m\right)=2A_m$$

⇒Am=Amax−Amin2$\Rightarrow A_m=\frac{A_{max}-A_{min}}{2}$ (Equation 7)

The ratio of Equation 7 and Equation 6 will be as follows.

AmAc=(Amax−Amin)/2(Amax+Amin)/2$$\frac{A_m}{A_c}=\frac{\left(A_{max}-A_{min}\right)/2}{\left(A_{max}+A_{min}\right)/2}$$

⇒μ=Amax−AminAmax+Amin$\Rightarrow \mu =\frac{A_{max}-A_{min}}{A_{max}+A_{min}}$ (Equation 8)

Therefore, Equation 3 and Equation 8 are the two formulas for Modulation index. The modulation index or modulation depth is often denoted in percentage called as Percentage of Modulation. We will get the percentage of modulation, just by multiplying the modulation index value with 100.

For a perfect modulation, the value of modulation index should be 1, which implies the percentage of modulation should be 100%.

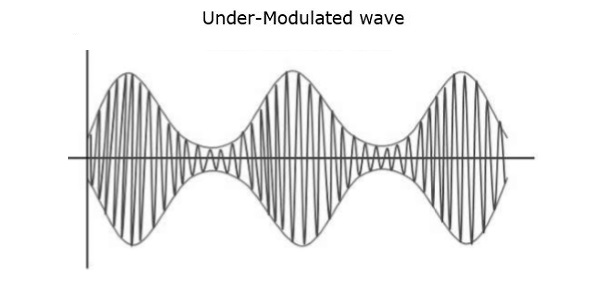
For instance, if this value is less than 1, i.e., the modulation index is 0.5, then the modulated output would look like the following figure. It is called as Under-modulation. Such a wave is called as an under-modulated wave.

If the value of the modulation index is greater than 1, i.e., 1.5 or so, then the wave will be an over-modulated wave. It would look like the following figure.

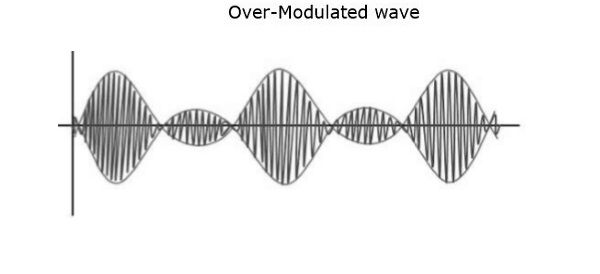
As the value of the modulation index increases, the carrier experiences a 180^ophase reversal, which causes additional sidebands and hence, the wave gets distorted. Such an over-modulated wave causes interference, which cannot be eliminated.

Bandwidth of AM Wave

Bandwidth (BW) is the difference between the highest and lowest frequencies of the signal. Mathematically, we can write it as

BW=fmax−fmin$$BW=f_{max}-f_{min}$$

Consider the following equation of amplitude modulated wave.

s(t)=Ac[1+μcos(2πfmt)]cos(2πfct)$$s\left(t\right)=A_c\left[1+\mu \cos \left(2\pi f_{m}t\right)\right]\cos \left(2\pi f_{c}t\right)$$

⇒s(t)=Accos(2πfct)+Acμcos(2πfct)cos(2πfmt)$$\Rightarrow s\left(t\right)=A_c\cos \left(2\pi f_{c}t\right)+A_c\mu \cos (2\pi f_{c}t)\cos \left(2\pi f_{m}t\right)$$

⇒s(t)=Accos(2πfct)+Acμ2cos[2π(fc+fm)t]+Acμ2cos[2π(fc−fm)t]$\Rightarrow s\left(t\right)=A_c\cos \left(2\pi f_{c}t\right)+\frac{A_c\mu }{2}\cos \left[2\pi \left(f_c+f_m\right)t\right]+\frac{A_c\mu }{2}\cos \left[2\pi \left(f_c-f_m\right)t\right]$

Hence, the amplitude modulated wave has three frequencies. Those are carrier frequency fc$f_c$, upper sideband frequency fc+fm$f_c+f_m$ and lower sideband frequency fc−fm$f_c-f_m$

Here,

fmax=fc+fm$f_{max}=f_c+f_m$ and fmin=fc−fm$f_{min}=f_c-f_m$

Substitute, fmax$f_{max}$ and fmin$f_{min}$ values in bandwidth formula.

BW=fc+fm−(fc−fm)$$BW=f_c+f_m-\left(f_c-f_m\right)$$

⇒BW=2fm$$\Rightarrow BW=2f_m$$

Thus, it can be said that the bandwidth required for amplitude modulated wave is twice the frequency of the modulating signal.

Power Calculations of AM Wave

Consider the following equation of amplitude modulated wave.

 s(t)=Accos(2πfct)+Acμ2cos[2π(fc+fm)t]+Acμ2cos[2π(fc−fm)t]$s\left(t\right)=A_c\cos \left(2\pi f_{c}t\right)+\frac{A_c\mu }{2}\cos \left[2\pi \left(f_c+f_m\right)t\right]+\frac{A_c\mu }{2}\cos \left[2\pi \left(f_c-f_m\right)t\right]$

Power of AM wave is equal to the sum of powers of carrier, upper sideband, and lower sideband frequency components.

Pt=Pc+PUSB+PLSB$$P_t=P_c+P_{USB}+P_{LSB}$$

We know that the standard formula for power of cos signal is

P=vrms2R=(vm/2–√)22$$P=\frac{{v_{rms}}^2}{R}=\frac{{\left(v_m/\sqrt{2}\right)}^2}{2}$$

Where,

vrms$v_{rms}$ is the rms value of cos signal.

vm$v_m$ is the peak value of cos signal.

First, let us find the powers of the carrier, the upper and lower sideband one by one.

Carrier power

Pc=(Ac/2–√)2R=Ac22R$$P_c=\frac{{\left(A_c/\sqrt{2}\right)}^2}{R}=\frac{{A_c}^2}{2R}$$

Upper sideband power

PUSB=(Acμ/22–√)2R=Ac2μ28R$$P_{USB}=\frac{{\left(A_c\mu /2\sqrt{2}\right)}^2}{R}=\frac{{A_c}^2{{}_{\mu }}^2}{8R}$$

Similarly, we will get the lower sideband power same as that of the upper side band power.

PLSB=Ac2μ28R$$P_{LSB}=\frac{{A_c}^2{{}_{\mu }}^2}{8R}$$

Now, let us add these three powers in order to get the power of AM wave.

Pt=Ac22R+Ac2μ28R+Ac2μ28R$$P_t=\frac{{A_c}^2}{2R}+\frac{{A_c}^2{{}_{\mu }}^2}{8R}+\frac{{A_c}^2{{}_{\mu }}^2}{8R}$$

⇒Pt=(Ac22R)(1+μ24+μ24)$$\Rightarrow P_t=\left(\frac{{A_c}^2}{2R}\right)\left(1+\frac{{\mu }^2}{4}+\frac{{\mu }^2}{4}\right)$$

⇒Pt=Pc(1+μ22)$$\Rightarrow P_t=P_c\left(1+\frac{{\mu }^2}{2}\right)$$

We can use the above formula to calculate the power of AM wave, when the carrier power and the modulation index are known.

If the modulation index μ=1$\mu =1$ then the power of AM wave is equal to 1.5 times the carrier power. So, the power required for transmitting an AM wave is 1.5 times the carrier power for a perfect modulation.