Add or Subtract Fractions With Different Denominators: Advanced

Introduction

When we have addition or subtraction of fractions with unlike denominators, we first find the Least Common Denominator (LCD) of the fractions. We then rewrite all fractions as equivalent fractions with LCD as the denominator. Now that all denominators are alike, we add or subtract the numerators and put the result over the common denominator to get the answer. If necessary, we express the fraction in lowest terms.

Problem 1:

Add 35$\frac{3}{5}$ + 38$\frac{3}{8}$

Solution

Step 1:

Add 35$\frac{3}{5}$ + 38$\frac{3}{8}$

Here the denominators are different. The LCD is 40 (product of 5 and 8) as 5 and 8 are co-prime numbers.

Step 2:

Rewriting

35$\frac{3}{5}$ + 38$\frac{3}{8}$ = (3×8)(5×8)$\frac{(3\times 8)}{(5\times 8)}$ + (5×5)(8×5)$\frac{(5\times 5)}{(8\times 5)}$ = 2440$\frac{24}{40}$ + 2540$\frac{25}{40}$

As the denominators have become equal

2440$\frac{24}{40}$ + 2540$\frac{25}{40}$ = (24+25)40$\frac{(24+25)}{40}$ = 4940$\frac{49}{40}$

Step 3:

So, 35$\frac{3}{5}$ + 38$\frac{3}{8}$ = 4940$\frac{49}{40}$

Problem 2:

Subtract 58$\frac{5}{8}$ − 712$\frac{7}{12}$

Solution

Step 1:

58$\frac{5}{8}$ − 712$\frac{7}{12}$

Here the denominators are different. The LCD here is 24.

Step 2:

Rewriting

58$\frac{5}{8}$ − 712$\frac{7}{12}$ = (5×3)(8×3)$\frac{(5\times 3)}{(8\times 3)}$ − (7×2)(12×2)$\frac{(7\times 2)}{(12\times 2)}$ = 1524$\frac{15}{24}$ − 1424$\frac{14}{24}$

As the denominators have become equal

1524$\frac{15}{24}$ − 1424$\frac{14}{24}$ = (15−14)24$\frac{(15-14)}{24}$ = 124$\frac{1}{24}$

Step 3:

So, 58$\frac{5}{8}$ − 712$\frac{7}{12}$ = 124

Word Problem Involving Add or Subtract Fractions With Different Denominators

Problem 1:

Jamie bought a box of fruit weighing 325$\frac{2}{5}$ kilograms. If she bought a second box that weighed 713$\frac{1}{3}$ kilograms, what is the combined weight of both boxes?

Solution

Step 1:

Weight of the first box of fruit = 325$\frac{2}{5}$ kilograms

Weight of the second box of fruit = 713$\frac{1}{3}$ kilograms

The combined of the two boxes of fruit = 325$\frac{2}{5}$ + 713$\frac{1}{3}$ = 175$\frac{17}{5}$ + 223$\frac{22}{3}$

Step 2:

The denominators are different. So the LCD of the fractions or LCM of denominators 3 and 5 is 15.

Rewriting to get equivalent fractions with LCD as denominator

17×35×3$\frac{17\times 3}{5\times 3}$ + 22×53×5$\frac{22\times 5}{3\times 5}$ = 5115$\frac{51}{15}$ + 11015$\frac{110}{15}$ = (51+110)15$\frac{(51+110)}{15}$ = 16115$\frac{161}{15}$ = 101115$\frac{11}{15}$

Problem 2:

During the weekend, Nancy spent a total 513$\frac{1}{3}$ hours studying. If she spent 314$\frac{1}{4}$ hours studying on Saturday, how long did she study on Sunday?

Solution

Step 1:

Time spent studying on the weekend = 513$\frac{1}{3}$ hours

Time spent studying on Saturday = 314$\frac{1}{4}$ hours

Time spent studying on Sunday =

Time spent studying on the weekend − Time spent studying on Saturday

= 513$\frac{1}{3}$ − 314$\frac{1}{4}$ = 163$\frac{16}{3}$ − 134$\frac{13}{4}$

Step 2:

LCD of the fractions or the LCM of the denominators 3 and 4 is 12

Rewriting to get equivalent fractions with LCD as denominator

16×43×4$\frac{16\times 4}{3\times 4}$ − 13×34×3$\frac{13\times 3}{4\times 3}$ = 6412$\frac{64}{12}$ − 3912$\frac{39}{12}$ = 64−3912$\frac{64-39}{12}$ = 2512$\frac{25}{12}$ = 2112$\frac{1}{12}$ hours

So, the time spent studying on Sunday = 2112$\frac{1}{12}$ hours

Problem 3:

Marcos bought apples that weighed 623$\frac{2}{3}$ kilograms. If he gave away 315$\frac{1}{5}$kilograms of apples to his friends, how many kilograms of apples does he have left?

Solution

Step 1:

Weight of the apples bought = 623$\frac{2}{3}$ kilograms

Weight of the apples given to friends = 315$\frac{1}{5}$ kilograms

Weight of the apples left =

Weight of the apples bought − Weight of the apples given to friends

= 623$\frac{2}{3}$ − 315$\frac{1}{5}$ = 203$\frac{20}{3}$ − 165$\frac{16}{5}$

Step 2:

LCD of the fractions or LCM of the denominators 3 and 5 is 15

Rewriting to get equivalent fractions with LCD as denominator

20×53×5$\frac{20\times 5}{3\times 5}$ − 16×35×3$\frac{16\times 3}{5\times 3}$ = 10015$\frac{100}{15}$ − 4815$\frac{48}{15}$ = 100−4815$\frac{100-48}{15}$ = 5215$\frac{52}{15}$ = 3715$\frac{7}{15}$ kilograms

So, the weight of the apples left = 3715$\frac{7}{15}$ kilograms

Fractional Part of a Circle

Definition

A complete or whole circle is taken as 1 and parts of the circles are represented as fractions. For example, if a circle is divided into 8 equal parts, each of the parts represents the fraction 1/8. Three parts of such a circle would represent 3/8 and on.
Here we are dealing with a type of problems, where fractions representing certain parts in a circle are given and we are required to find the fraction representing the remaining unknown part of the circle. To solve such problems, we add up the fractions representing the fractional parts and then subtract the sum from 1, the whole circle. The result gives the fraction representing the unknown fractional part of the circle.

Problem 1:

How much of the circle is unshaded? Write your answer as a fraction in simplest form.

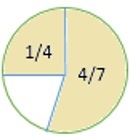
Solution

Step 1:

First we find what total part of figure is shaded.

14$\frac{1}{4}$ + 47$\frac{4}{7}$ = 728$\frac{7}{28}$ + 1628$\frac{16}{28}$ = (7+16)28$\frac{(7+16)}{28}$ = 2328$\frac{23}{28}$

Step 2:

To find the fraction of the figure that is unshaded we subtract the result we got (2328$\frac{23}{28}$) from 1.

1 − 2328$\frac{23}{28}$ = 2828$\frac{28}{28}$ − 2328$\frac{23}{28}$ = (28−2328$\frac{(28-23}{28}$ = 528$\frac{5}{28}$

So, the fraction of the figure that is unshaded is 528$\frac{5}{28}$.

Problem 2:

How much of the circle is shaded? Write your answer as a fraction in simplest form.

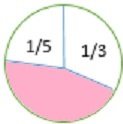
Solution

Step 1:

First we figure out how much of the figure is unshaded.

15$\frac{1}{5}$ + 13$\frac{1}{3}$ = 315$\frac{3}{15}$ + 515$\frac{5}{15}$ = (3+5)15$\frac{(3+5)}{15}$ = 815$\frac{8}{15}$

Step 2:

To find the fraction of the figure that is unshaded we subtract the result we got (815$\frac{8}{15}$) from 1.

1 − 815$\frac{8}{15}$ = 1515$\frac{15}{15}$ − 815$\frac{8}{15}$ = (15−8)15$\frac{(15-8)}{15}$ = 715$\frac{7}{15}$

So, the fraction of the figure that is shaded is 715$\frac{7}{15}$.

Add and Subtract Fractions

This tutorial provides comprehensive coverage of adding and subtracting of fractions based on Common Core (CCSS) and State Standards and its prerequisites. Students can navigate learning paths based on their level of readiness. Institutional users may customize the scope and sequence to meet curricular needs. This simple tutorial uses appropriate examples to help you understand adding and subtracting of fractions in a general and quick way.

Audience

This tutorial has been prepared for beginners to help them understand the basics of adding and subtracting of fractions. After completing this tutorial, you will find yourself at a moderate level of expertise in adding and subtracting of fractions, from where you can advance further.

Prerequisites

Before proceeding with this tutorial, you need a basic knowledge of elementary math concepts such as number sense, addition, subtraction, multiplication, division, whole numbers, fractions, equivalent fractions, least common denominator and so on.